

La règle dite d’or, aussi appelée divine proportion, est un rapport mathématique permettant la réparation harmonieuse des lignes et des surfaces dans une composition. Utilisée depuis l’Antiquité, elle correspond à la recherche de rapport idéal observé dans la nature :
(1+√5) ÷ 2 = 1.618 = 8 ÷ 5 = 5 ÷ 3.
Vitruve, architecte romain, définit cette règle esthétique comme suit : « Pour qu’un espace, divisé en parties inégales, apparaisse agréable et esthétique, il devra exister entre la partie la plus petite et la plus grande partie la même relation qu’entre cette dernière et l’ensemble. ». Le nombre d’or détermine un rapport entre deux segments de longueurs différentes déduit de forme géométriques que les Pythagoriciens considéraient comme parfaites : le carré et le cercle.
Comment obtenir le nombre d’or ? A partir d’un carré ABCD, placer le point M au milieu d’AB. Tracer le segment MC. Reporter à l’aide d’un compas le segment MC en MC’ sur la droite passant par A et B. Les segments AB et BC’ sont de rapport 1,618.
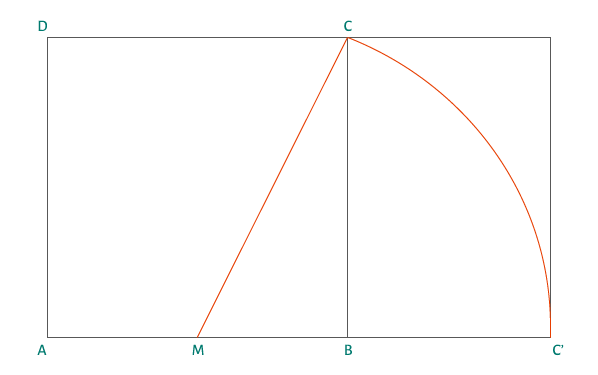
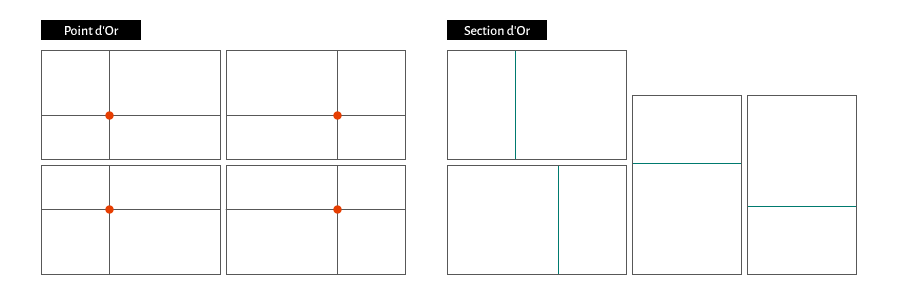
Le nombre d’or permet de définir des sections d’or ou des points d’or vers lesquels le regard converge naturellement. Aujourd’hui cette règle est toujours d’actualité même si on la retrouve le plus souvent de manière simplifiée : règle des tiers, proportions voisine : 8/5, 5/3).
Intrigué par la section d’or, Gustav Fechner, psychologue allemand de la fin du XIXème siècle, a étudié les réactions de l’homme face aux qualités esthétiques particulières du rectangle d’or. En effet, plusieurs indices tendaient à démontrer la préférence esthétique archétypale et transculturelle en faveur des proportions dérivées du nombre d’or. Les travaux de Fechner se sont limités à l’environnement fabriqué par l’homme. Il a commencé par mesurer plusieurs milliers d’objets rectangulaires, livres, boîtes, bâtiments, pochettes d’allumettes, journaux, etc. Fechner a découvert que les proportions d’un rectangle moyen étaient proches d’un rapport connu sous le nom de section d’or (1/1.618) et qu’une majorité de gens préférait un rectangle dont les proportions s’approchaient de la section d’or. Les travaux de Fechner ont, par la suite, été repris d’une manière plus scientifique par Lalo en 1908, puis par d’autres, pour aboutir à des résultats étonnamment semblables.
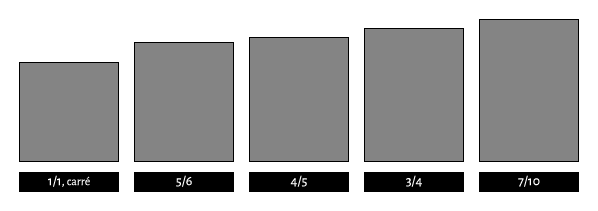
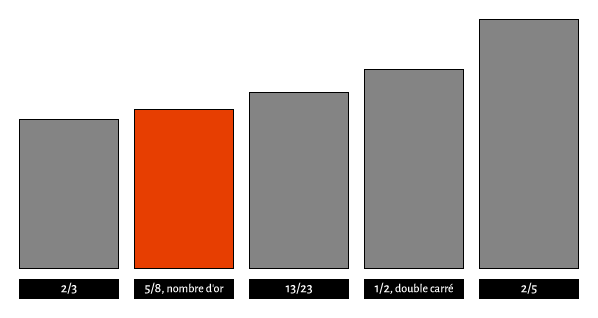
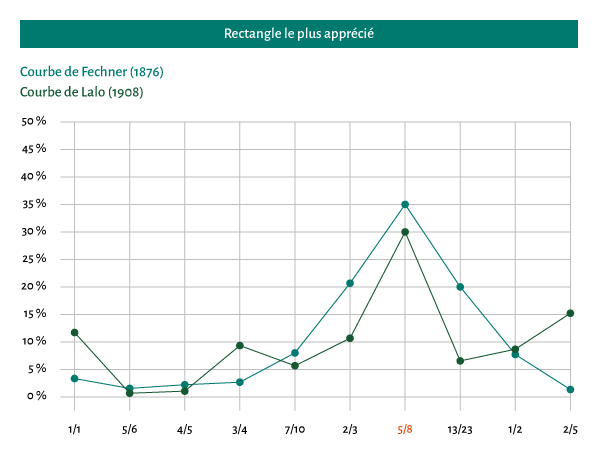
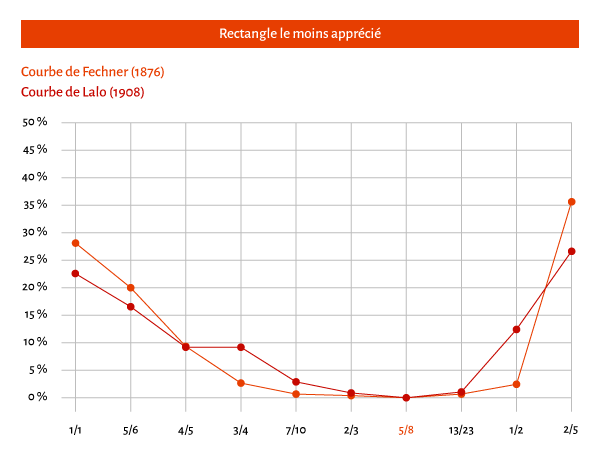
Source : « Géométrie du design » de Kimberly Elam, chez Eyrolles – « Mise en page, etc. » de Damien et Claire Gautier, chez Pyramyd.